阻抗匹配什么意思?阻抗匹配(impedance matching)指通过调整输入阻抗和输出阻抗来使得电子器件满足一定条件,通常该条件是使得系统传输功率最大或者使得信号反射最小。例如,再无线传输系统中需要匹配射频发射设备和接受天线的阻抗以此来实现传输功率最大化。 阻抗匹配的作用 · 实现最大功率传输:对信号源和负载进行阻抗匹配,可以实现传输功率最大化,提高能量转换性能; · 实现最小反射损耗:匹配阻抗可以减少信号在电路中的反射,提高信号质量和传输效率; · 优化系统性能:阻抗匹配可以确保信号在系统中的稳定传输,避免信号失真和性能下降。阻抗匹配对于获得理想的 VSWR(电压驻波比)非常重要。 · 在PCB测试中,减少高频噪声以及边沿过冲。如果一个信号的边沿非常陡峭,则含有大量的高频成分,将会辐射干扰,另外,也容易产生过冲。串联电阻与信号线的分布电容以及负载输入电容等形成一个RC电路,这样就会降低信号边沿的陡峭程度。还可以减少高频反射以及自激振荡。当信号的频率很高时,则信号的波长就很短,当波长短得跟传输线长度可以比拟时,反射信号叠加在原信号上将会改变原信号的形状。如果传输线的特征阻抗跟负载阻抗不相等(即不匹配)时,在负载端就会产生反射,造成自激振荡。PCB板内走线的低频信号直接连通即可,一般不需要加串行匹配电阻。 当阻抗不匹配时,就要通过阻抗变换使负载阻抗和源阻抗相等,以减小反射。经常是使用史密斯圆图阻抗匹配。反射系数是一个矢量,所以反射系数相同的点会形成一个圆,一系列反射系数形成反射圆图。 反射圆图上的每一个点都有唯一的阻抗特性,这样反射圆图和阻抗圆图重叠形成史密斯圆图。 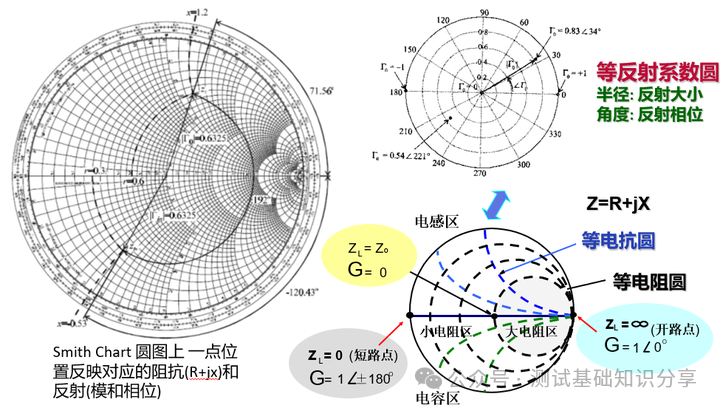 R值表示等电阻圆, Z值表示等电抗圆有, 交点为Z,该点半径为反射系数模值,夹角为反射系数相位。 请参考右下方的史密斯圆图,上面左边的点表示短路点,阻抗为0,反射系数是1,发生全反射,反射角为180度。中间点为匹配点,阻抗为特性阻抗,反射系数为0。右边点位开路点,阻抗无穷大,反射系数为1,同样也发生全反射,反射角为0度。上面是电感区,下面是电容区,然后上面还有等电阻圆,等点抗圆,等电导圆等等。 注意: 阻抗用直坐标系的话,需要看到无穷大的阻抗横轴和虚部纵轴,在仪表里显示是不现实的,所以用圆图。 圆图的周期为传输线信号波长/2。圆图旋转一圈代表传输线传输电长度为l/2,半圈为l/4。 史密斯圆图 The Smith Chart 贝尔实验室工程师菲利普·史密斯 (Phillip Smith) 设计了一种图解法,用于求解微波理论中常见的重复方程式。 例如反射系数方程式 Γ = (Z – 1)/(Z + 1)。由于该方程式中的所有值都是复数,因此使用史密斯图解法可以简化求解该表达式的繁琐过程。 该图本质上是两个平面——Z(或阻抗)平面和 Γ(或反射系数)平面——之间的映射。我们都熟悉阻抗平面——一个具有实轴和虚轴的直角坐标平面。任何阻抗都可以绘制在这个平面上。在本讨论中,我们将阻抗平面归一化为特性阻抗。 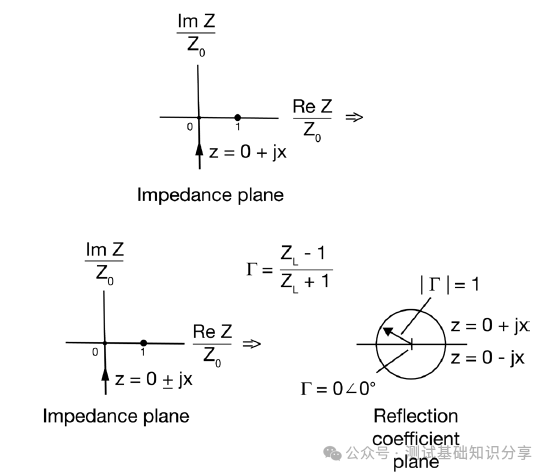 让我们在这个归一化平面中选取几个值,看看它们如何映射到 Γ 平面。令 z = 1。在 50 欧姆系统中,这意味着 Z = 50 欧姆。对于这个值,|Γ| = 0,即Γ平面的中心。 现在我们令z为纯虚数(即z = jx,其中x可以从负无穷到正无穷变化)。由于Γ = (jx – 1)/(jx + 1),|Γ| = 1,其相位角在0到360度之间变化。这在Γ平面上描绘出一个圆(图29)。对于正电抗,即jx为正,阻抗映射到上半圆。对于负电抗,阻抗映射到下半圆。上半圆区域为感性区域,下半圆区域为容性区域。 现在让我们看一些其他的阻抗值。一条通过实轴上z = 1点的恒阻线,在Γ平面上映射成一个圆。 上半圆表示阻抗为1 + jx,即感性区域; 下半圆表示阻抗为1 - jx,即容性区域。 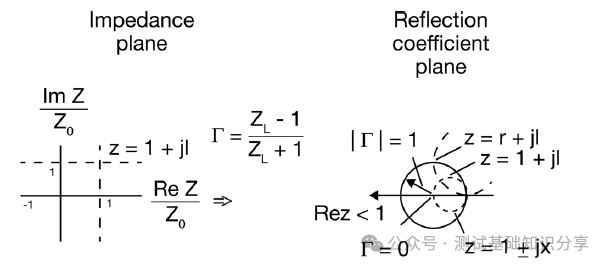 恒电抗线 r + j1 也以圆的形式映射到 Γ 平面上。当我们接近阻抗平面的虚轴时,Γ 接近单位半径圆。当我们穿过虚轴时,Γ 平面上的恒电抗圆会超出单位半径圆。 现在我们回过头来观察 z 的实数,我们可以看到在 z = -1 处,Γ = ∞。当 z 为实数且小于 1 时,我们会向外移动到 Γ 平面上的单位半径圆。当 z 的实部变为负值时,Γ 会继续沿着这个半径无限大的圆移动。单位半径圆外的整个区域表示实部为负的阻抗。稍后我们将在处理晶体管和其他通常具有负实数阻抗的有源器件时用到这个事实。 在阻抗平面上,恒电阻线和恒电抗线相交。它们也会在 Γ 平面上相交。阻抗平面上的点与 Γ 平面上的点之间存在一一对应关系。 通过继续绘制其他恒定电阻和电抗圆,就可以完成史密斯圆图。 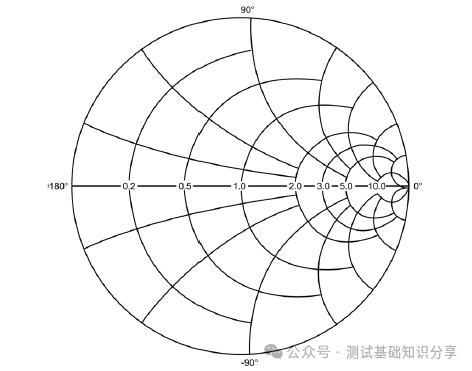 史密斯圆图的应用 Applications of the Smith Chart 现在让我们尝试用史密斯圆图举几个例子来说明它的实用性。 1. 阻抗到导纳的转换 将归一化阻抗 1 + j1 转换为导纳可以很容易地完成。让我们首先在史密斯圆图上绘制表示 z 值的点(图)。从这些关系中,我们可以看出,虽然导纳的大小是阻抗大小的倒数,但 Γ 的大小相同,但其相位角改变了 180 度。在史密斯圆图上,Γ 矢量将旋转 180 度。然后可以将该点读作导纳。 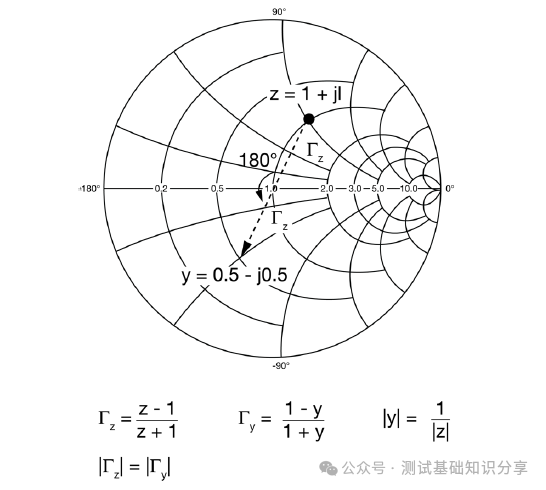 我们可以用另一种方法实现阻抗到导纳的转换。与其将 Γ 矢量旋转180度,不如将史密斯圆图旋转180度。我们可以将旋转后的圆图称为导纳图,将原始圆图称为阻抗图。这样,我们就可以直接将任何阻抗转换为导纳,反之亦然。 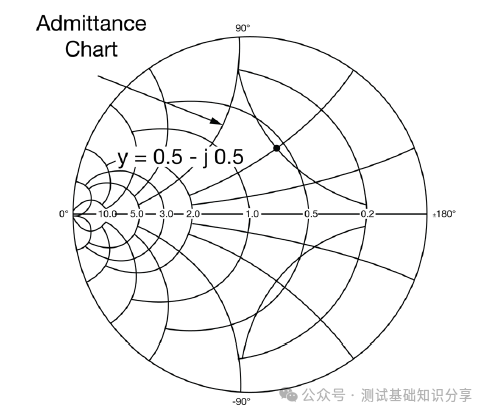 2. 实部为负的阻抗 现在我们来看看实部为负的阻抗。这又是一个传统的史密斯圆图,由单位半径圆的边界定义。如果一个阻抗是电感性的,且实部为负,它将映射到图外的 Γ 平面。将这个点重新映射到图上的一种方法是绘制Γ的倒数,而不是Γ本身。这很不方便,因为相位角不会保留。电感性阻抗的映射看起来似乎是电容性的。 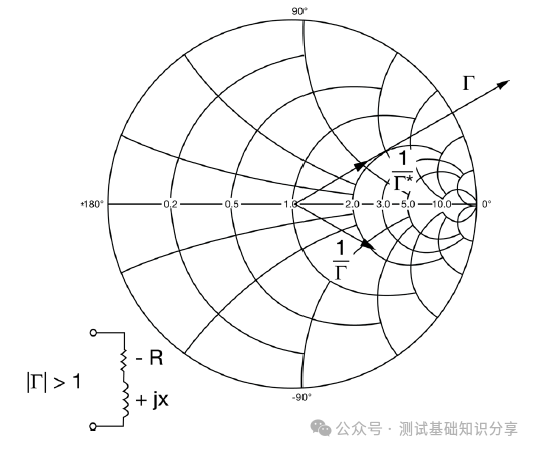 然而,如果我们绘制 Γ 的复共轭倒数,相位角保持不变。该值与原始 Γ 位于同一条线上。 此外,还有史密斯圆图压缩,其中包含单位半径图以及大量的负阻抗区域。该图的半径对应于幅度为3.16的反射系数。 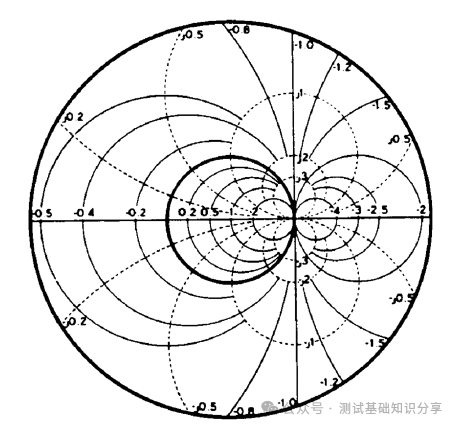 3. 频率响应 我们来看一个阻抗为 z = 0.4 + jx 的网络。随着输入信号频率的增加,该网络的阻抗图沿着阻抗值为 0.4 的恒阻圆顺时针移动。这种随着频率增加而顺时针移动的现象是无源网络史密斯圆图上阻抗图的典型特征。这本质上就是福斯特电抗定理。 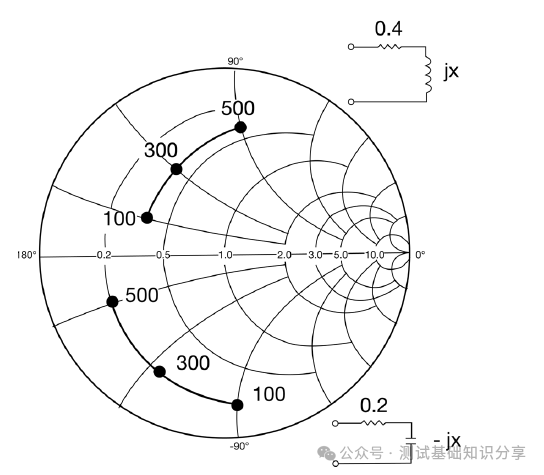 现在,如果我们看另一个实部为 0.2 且虚部为容性的电路,则阻抗图会随着频率的增加再次顺时针移动。另一种经常遇到的电路是谐振电路。此时,史密斯圆图也可用于绘制频率响应(图)。 对于零频率下的该电路,电感器是短路的。我们从点 z = 0 开始绘制。随着频率的增加,感抗占主导地位。我们顺时针移动。在谐振时,阻抗为纯实数,具有电阻器的值。如果电阻器具有更高的值,则谐振时的交叉点将在史密斯圆图上更靠右的位置。随着频率继续增加,响应顺时针移动到史密斯圆图的容性区域,直到达到无限大频率,此时阻抗再次为零。 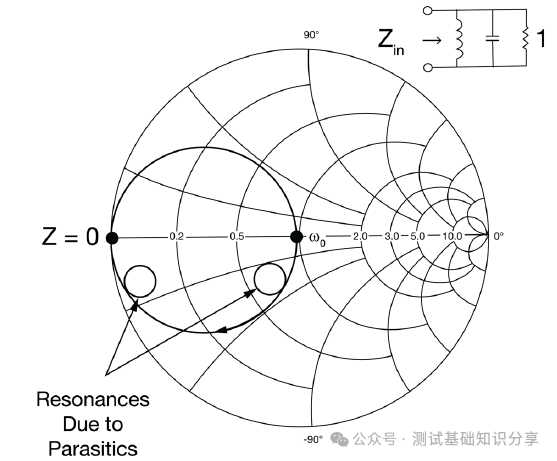 理论上,谐振电路的完整响应应该是一个圆。实际上,由于我们通常不会在整个频率范围内都使用纯电容或纯电感元件,因此我们会看到其他小圆环,这些圆环指示其他谐振。这可能是由于电容器中的寄生电感或电感器中的寄生电容引起的。这些圆的直径在某种程度上可以指示电路的Q值。如果我们有一个理想的谐振电路,其响应应该是史密斯圆图上的外圆。这表示Q值无穷大。 还有其他使用史密斯圆图测量腔体和YIG球的Q值的技术。其中一种技术利用了这样一个事实:在谐振电路中,电路的实部在半功率点处等于无功部分。让我们在史密斯圆图上画两条连接这些点的圆弧。 这些圆弧的圆心在 j1处。圆弧的半径为√2 . 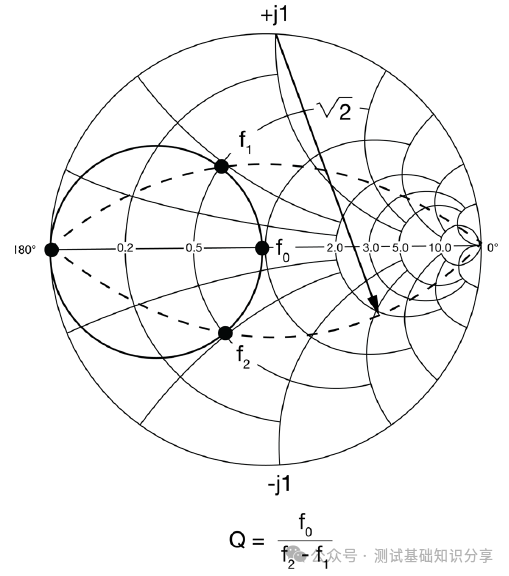 然后,我们增加频率,并记录响应位于上圆弧时的频率值。继续增加频率,记录谐振频率和响应位于下圆弧时的频率。电路的Q值公式很简单,就是谐振频率fo除以上下半功率点之间的频率差。Q = fo/Δf。 什么是福斯特电抗定理? 福斯特电抗定理(Foster's Reactance Theorem)是描述无源无耗一端口网络中输入电抗和电纳随频率变化的规律,指出二者均为频率的严格单调递增函数。 福斯特电抗定理的核心内容 福斯特电抗定理的核心观点是:对于一个无源无耗一端口网络,其输入电抗(XX)和电纳(BB)均是频率的严格单调递增函数。这意味着: 随着频率升高,电抗值必然增大; 电纳(电抗的倒数)同样随频率单调递增。 福斯特电抗定理的应用场景: 该定理常用于分析LC电路、谐振腔等无耗网络的频率响应特性。 测试和测量: 虽然该定理本身是一项基本原理,但它可以通过多种方式进行测试和测量: 单端口网络 - 可以通过确定不同频率下输入阻抗或导纳的虚部直接测量电抗。 双端口网络 - 可以从双端口网络参数(例如 Z 参数、Y 参数或 S 参数)中提取电抗。 仿真与分析 - 网络仿真器可用于分析拟议网络设计的频率响应,并验证其是否符合福斯特定理的要求。 Q因子估算 - 该定理可用于估算谐振器的 Q因子,Q因子是衡量能量存储和损耗的指标。 本质上,测试福斯特电抗定理涉及验证无源无损网络的测量电抗函数是否与频率呈现严格的递增关系。这对于确保网络设计在物理上可实现且性能符合预期至关重要。 总结 让我们快速回顾一下我们在史密斯圆图上看到的内容。它是阻抗平面和反射系数(或Γ平面)的映射。 我们发现,实部为正的阻抗映射到史密斯圆图的单位半径圆内。实部为负的阻抗映射到该单位半径圆外。实部为正且具有感抗的阻抗映射到史密斯圆图的上半部分。容抗的阻抗映射到史密斯圆图的下半部分。 如何用史密斯圆图进行阻抗测试? 作为一款应用于电机与电子工程学的经典图表,史密斯圆图被广泛用于阻抗匹配、电路调试、参数计算甚至滤波器调试等用,今天我们将展示其中非常经典的矢量网分仪阻抗测试方法。 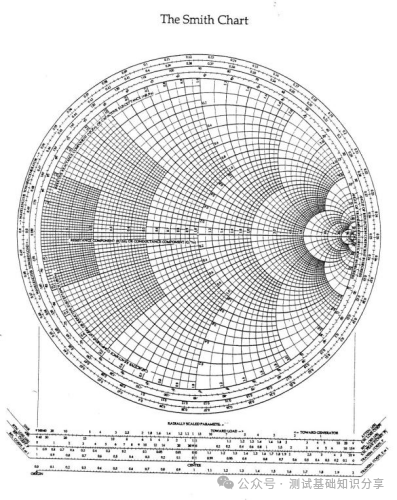 首先,我们先挑选网络分析仪: 在测试之前必不可少的工作,便是对仪器进行校准。E5071C ENA 矢量网络分析仪 在测试之前必不可少的工作,便是对仪器进行校准。  首先,我们在数据格式上选择史密斯圆图。 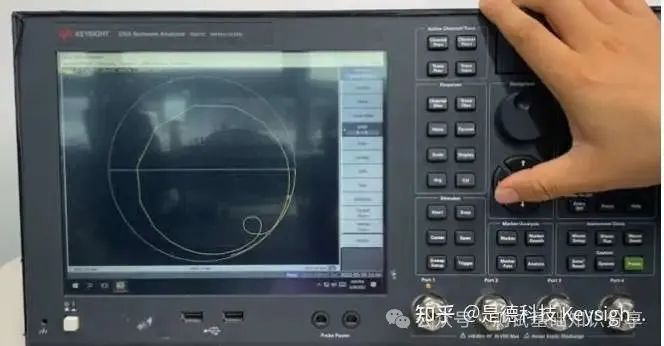 然后,我们用校准件上的一个负载(阻抗50欧姆)。  我们再接上负载校准件。  设置一个marker点。  我们可以看到史密斯圆图测出来的阻值50欧姆。 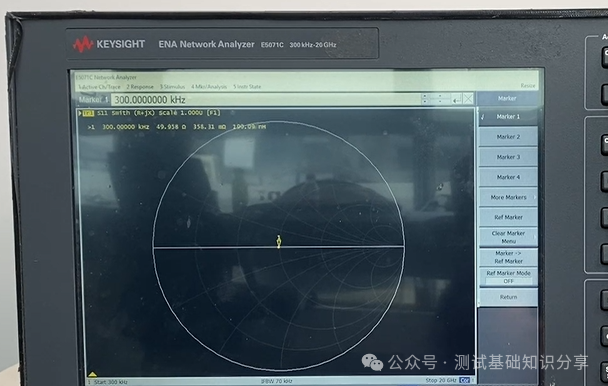 以上便是“史密斯圆图阻抗测量”的详细方法,如果仍有不清楚的地方,您可以 |





